Математика в Древнем Вавилоне

Из более 500 тыс. глиняных табличек, найденных археологами при раскопках в Древней Месопотамии, около 400 содержат математические сведения. Большинство из них расшифрованы и позволяют составить довольно ясное представление о поразительных алгебраических и геометрических достижениях вавилонских учёных.

О времени и месте рождения математики мнения разнятся. Многочисленные исследователи этого вопроса приписывают создание её различным народам и приурочивают к разным эпохам. Единой точки зрения на этот счёт не было ещё у древних греков, среди которых особенно была распространена версия, что геометрию придумали египтяне, а арифметику — финикийские купцы, которые нуждались в подобных знаниях для торговых расчётов. Геродот в «Истории» и Страбон в «Географии» отдавали приоритет финикийцам. Платон и Диоген Лаэрций родиной и арифметики, и геометрии считали Египет. Таково же и мнение Аристотеля, полагавшего, что математика зародилась благодаря наличию досуга у тамошних жрецов.

Это замечание следует за пассажем о том, что в каждой цивилизации сначала рождаются практические ремёсла, затем искусства, служащие удовольствию, и лишь затем науки, направленные на познание. Евдем, ученик Аристотеля, как и большинство его предшественников, также считал родиной геометрии Египет, а причиной её появления — практические потребности землемерия. В своём совершенствовании геометрия проходит, по Евдему, три этапа: зарождение практических навыков землемерия, появление практически ориентированной прикладной дисциплины и превращение её в теоретическую науку. Судя по всему, два первых этапа Евдем относил к Египту, а третий — к греческой математике. Правда, он всё же признавал, что теория вычисления площадей возникла из решения квадратных уравнений, имевших вавилонское происхождение.

Небольшие глиняные бляшки, найденные в Иране, предположительно использовались для записи мер зерна 8 тыс. до н.э. Норвежский институт палеографии и истории, Осло.

У историка Иосифа Флавия («Древняя Иудея», кн. 1, гл. 8) своё мнение. Он хоть и называет египтян первыми, но уверен, что арифметике и астрономии их обучил праотец евреев Авраам, скрывшийся в Египет во время голода, постигшего Ханаанскую землю. Что ж, египетское влияние в Греции было достаточно сильным, чтобы навязать грекам подобное мнение, которое с их лёгкой руки имеет хождение в исторической литературе до сих пор. Хорошо сохранившиеся глиняные таблички, покрытые клинописными текстами, найденные в Месопотамии и датируемые от 2000 г. до н.э. и до 300 г. н.э., свидетельствуют как о несколько ином положении дел, так и о том, что представляла собой математика в древнем Вавилоне. Это был довольно сложный сплав арифметики, алгебры, геометрии и даже начатков тригонометрии.

Математике учили в писцовых школах, и каждый выпускник обладал довольно серьёзным для того времени объёмом знаний. Видимо, именно об этом говорит Ашшурбанипал, царь Ассирии в 7 в. до н.э., в одной из своих надписей, сообщая, что научился находить «сложные обратные дроби и умножать». Прибегать к вычислениям, жизнь заставляла вавилонян на каждом шагу. Арифметика и нехитрая алгебра нужны были в ведении хозяйства, при обмене денег и расчётах за товары, вычислении простых и сложных процентов, налогов и доли урожая, сдаваемой в пользу государства, храма или землевладельца. Математических расчётов, причём довольно сложных, требовали масштабные архитектурные проекты, инженерные работы при строительстве ирригационной системы, баллистика, астрономия, астрология.

Важной задачей математики было определение сроков сельскохозяйственных работ, религиозных праздников, другие календарные нужды. Сколь высоки в древних городах-государствах междуречья Тигра и Евфрата были достижения в том, что греки позже назовут так удивительно точно mathema («познание»), позволяют судить расшифровки месопотамских глиняных клинописей. К слову, у греков термин mathema поначалу обозначал перечень четырёх наук: арифметику, геометрию, астрономию и гармонику, собственно математику он начал обозначать много позже. В Месопотамии археологи уже нашли и продолжают находить клинописные таблички с записями математического характера частью на аккадском, частью на шумерском языках, а также справочные математические таблицы. Последние сильно облегчали вычисления, которые приходилось производить повседневно, поэтому в ряде расшифрованных текстов довольно часто содержится исчисление процентов.

Сохранились названия арифметических действий более раннего, шумерского периода месопотамской истории. Так, операция сложения называлась «накопление» или «прибавление», при вычитании употреблялся глагол «вырывать», а термин для умножения означал «скушать». Интересно, что в Вавилоне пользовались более обширной таблицей умножения — от 1 до 180 000, чем та, которую пришлось учить в школе нам, т.е. рассчитанная на числа от 1 до 100. В Древней Месопотамии были созданы единообразные правила арифметических действий не только с целыми числами, но и с дробями, в искусстве оперирования которыми вавилоняне значительно превосходили египтян. В Египте, например, операции с дробями долгое время продолжали оставаться на примитивном уровне, так как они знали лишь аликвотные дроби (т.е. дроби с числителем, равным 1). Со времён шумеров в Месопотамии основной счётной единицей во всех хозяйственных делах было число 60, хотя была известна и десятеричная система счисления, которая была в ходу у аккадцев.

Самая знаменитая из математических табличек Старовавилонского периода, хранящаяся в библиотеке Колумбийского университета (США). Содержит перечень прямоугольных треугольников с рациональными сторонами, то есть троек пифагоровых чисел x2 + y2 = z2 и свидетельствует о том, что теорема Пифагора была известна вавилонянам не менее чем за тысячу лет до рождения её автора. 1900 — 1600 гг. до н.э.

Вавилонские математики широко пользовались шестидесятеричной позиционной(!) системой счёта. На её основе и были составлены различные вычислительные таблицы. Кроме таблиц умножения и таблиц обратных величин, с помощью которых производилось деление, существовали таблицы квадратных корней и кубических чисел. Клинописные тексты, посвящённые решению алгебраических и геометрических задач, свидетельствуют о том, что вавилонские математики умели решать некоторые специальные задачи, включавшие до десяти уравнений с десятью неизвестными, а также отдельные разновидности кубических уравнений и уравнений четвёртой степени. Квадратные уравнения вначале служили, в основном, сугубо практическим целям — измерению площадей и объёмов, что отразилось на терминологии. Например, при решении уравнений с двумя неизвестными, одно называлось «длиной», а другое — «шириной». Произведение неизвестных называли «площадью». Как и сейчас!

В задачах, приводящих к кубическому уравнению, встречалась третья неизвестная величина — «глубина», а произведение трёх неизвестных именовалось «объёмом». В дальнейшем, с развитием алгебраического мышления, неизвестные стали пониматься более абстрактно. Иногда в качестве иллюстрации алгебраических соотношений в Вавилоне использовались геометрические чертежи. Позже, в Древней Греции они стали основным элементом алгебры, тогда как для вавилонян, мысливших, прежде всего, алгебраически, чертежи были лишь средством наглядности, и под терминами «линия» и «площадь» чаще всего понимались безразмерные числа. Потому-то и встречались решения задач, где «площадь» складывалась со «стороной» или отнималась от «объёма» и т.п. Особое значение имело в древности точное измерение полей, садов, строений — ежегодные разливы рек приносили большое количество ила, который покрывал поля и уничтожал межи между ними, и после спада воды землемерам по заказу их владельцев частенько приходилось вновь перемеривать наделы. В клинописных архивах сохранилось немало таких землемерных карт, составленных свыше 4 тыс. лет тому назад.

Первоначально единицы измерения были не очень точными, ведь длину измеряли пальцами, ладонями, локтями, которые у разных людей разные. Получше обстояло дело с большими величинами, для измерения которых пользовались тростником и верёвкой определённых размеров. Но и здесь результаты измерений нередко различались между собой, в зависимости от того, кто мерил и где. Поэтому в разных городах Вавилонии были приняты разные меры длины. Например, в городе Лагаше «локоть» был равен 400 мм, а в Ниппуре и самом Вавилоне — 518 мм. Многие сохранившиеся клинописные материалы представляли собой учебные пособия для вавилонских школьников, в которых приводились решения различных несложных задач, часто встречавшихся в практической жизни. Неясно, правда, решал ли ученик их в уме или делал предварительные вычисления прутиком на земле — на табличках записаны только условия математических задач и их решение.

Геометрические задачи с рисунками трапеций и треугольников и решением теоремы Пифагора. Размеры таблички: 21,0x8,2. 19 в. до н.э. Британский музей

Основную часть курса математики в школе занимало решение арифметических, алгебраических и геометрических задач, при формулировке которых было принято оперировать конкретными предметами, площадями и объёмами. На одной из клинописных табличек сохранилась такая задачка: «За сколько дней можно изготовить кусок ткани определённой длины, если мы знаем, что ежедневно изготовляется столько-то локтей (мера длины) этой ткани?» На другой приведены задачи, связанные со строительными работами. Например, «Сколько земли потребуется для насыпи, размеры которой известны, и сколько грунта должен перетаскать каждый рабочий, если известно их общее число?» или «Сколько глины должен заготовить каждый рабочий для возведения стены определённых размеров?»

Школьник также должен был уметь вычислять коэффициенты, подсчитывать итоги, решать задачи по измерению углов, вычислению площадей и объёмов прямолинейных фигур — это был обычный набор для элементарной геометрии. Интересны сохранившиеся с шумерских времён названия геометрических фигур. Треугольник назывался «клин», трапеция — «лоб быка», круг — «обруч», ёмкость обозначалась термином «вода», объём — «земля, песок», площадь именовалась «поле». Один из клинописных текстов содержит 16 задач с решениями, которые относятся к плотинам, валам, колодцам, водяным часам и земельным работам. Одна задача снабжена чертежом, относящимся к круговому валу, ещё одна рассматривает усечённый конус, определяя его объём умножением высоты на полусумму площадей верхнего и нижнего оснований.

Вавилонские математики решали также планиметрические задачи, используя свойства прямоугольных треугольников, сформулированные Пифагором впоследствии в виде теоремы о равенстве в прямоугольном треугольнике квадрата гипотенузы сумме квадратов катетов. Другими словами, знаменитая теорема Пифагора была известна вавилонянам не менее чем за тысячу лет до Пифагора. Помимо планиметрических задач, решали и стереометрические, связанные с определением объёма различного рода пространств, тел, широко практиковали черчение планов полей, местностей, отдельных зданий, но обычно не в масштабе. Наиболее значительным достижением математики было открытие того факта, что отношение диагонали и стороны квадрата не может быть выражено целым числом или простой дробью. Тем самым в математику было введено понятие иррациональности.

Считается, что открытие одного из важнейших иррациональных чисел — числа π, выражающего отношение длины окружности к её диаметру и равняющееся бесконечной дроби ≈ 3,14..., принадлежит Пифагору. По другой версии, для числа π значение 3,14 впервые предложил Архимед на 300 лет позже, в 3 в. до н.э. Ещё по одной, первым вычислившим его был Омар Хайям, это вообще 11 — 12 в. н.э. Достоверно известно лишь, что греческой буквой π это отношение впервые обозначил в 1706 г. английский математик Уильям Джонс, и лишь после того как в 1737 г. это обозначение позаимствовал швейцарский математик Леонард Эйлер, оно стало общепринятым. Число π — древнейшая математическая загадка, это открытие следует искать также в Древней Месопотамии.

Вавилонские математики прекрасно знали о важнейших иррациональных числах, и решение задачи по вычислению площади круга также можно найти в расшифровках клинописных глиняных табличек математического содержания. Согласно этим данным π принималось равным 3, что, впрочем, было вполне достаточно для практических землемерных целей. Исследователи считают, что шестидесятеричная система была выбрана в Древнем Вавилоне из метрологических соображений: число 60 имеет много делителей. Шестидесятеричная запись целых чисел распространения за пределами Месопотамии не получила, но в Европе вплоть до 17 в. широко применялись и шестидесятеричные дроби, и привычное нам деление окружности на 360 градусов. Час и минуты, делящиеся на 60 частей, также берут начало в Вавилоне.

Замечательна остроумная придумка вавилонян использовать для записи чисел минимальное количество цифровых знаков. Римлянам, например, даже в голову не пришло, что одной и той же цифрой можно обозначить разные величины! Для этого они использовали буквы своего алфавита. В итоге четырёхзначное число, к примеру, 2737 содержало аж одиннадцать букв: MMDCCXXXVII. И хотя и в наше время найдутся экстремалы-математики, которые сумеют разделить в столбик LXXVIII на CLXVI или перемножить CLIX на LXXIV, остаётся только пожалеть тех жителей Вечного города, которым приходилось производить при помощи подобной математической эквилибристики сложные календарные и астрономические расчёты или рассчитывались масштабные архитектурные проекты и различные инженерные объекты.

На использовании букв алфавита была основана и греческая система счисления. Вначале в Греции была принята аттическая система, использовавшая для обозначения единицы вертикальную черту, а для чисел 5, 10, 100, 1000, 10 000 (по существу это была десятичная система) — начальные буквы их греческих названий. Позже, примерно в 3 в. до н.э., получила широкое распространение ионическая система счисления, в которой для обозначения чисел использовались 24 буквы греческого алфавита и три архаические буквы. А чтобы отличить числа от слов, греки над соответствующей буквой ставили горизонтальную черту. В этом смысле вавилонская математическая наука стояла выше позднейших греческой или римской, так как именно ей принадлежит одно из самых выдающихся достижений в развитии систем обозначений чисел — принцип позиционности, согласно которому один и тот же числовой знак (символ) имеет различные значения в зависимости от того места, где он расположен. К слову, уступала вавилонской и современная ей египетская система счисления.

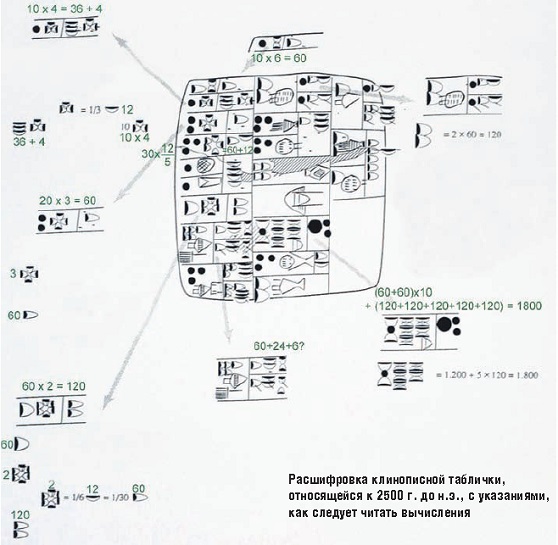
Табличка с вычислениями диаметра окружности из царской библиотеки Ашшурбанипала свидетельствует о том, что вавилонские математики умели решать задачи по вычислению площади круга и им было знакомо иррациональное число π.

17 в. до н.э. Частная коллекция

Египтяне пользовались непозиционной десятичной системой, в которой числа от 1 до 9 обозначались соответствующим числом вертикальных чёрточек, а для последовательных степеней числа 10 вводились индивидуальные иероглифические символы. Для малых чисел вавилонская система счисления в основных чертах напоминала египетскую. Одна вертикальная клинообразная черта (в раннешумерских табличках — небольшой полукруг) означала единицу; повторенный нужное число раз этот знак служил для записи чисел меньше десяти; для обозначения числа 10 вавилоняне, как и египтяне, ввели новый символ — широкий клиновидный знак с остриём, направленным влево, напоминающий по форме угловую скобку, (в раннешумерских текстах — небольшой кружок). Повторенный соответствующее число раз, этот знак служил для обозначения чисел 20, 30, 40 и 50. Большинство современных историков считает, что древние научные познания носили чисто эмпирический характер.

В отношении физики, химии, натурфилософии, в основе которых лежали наблюдения, вроде и верно. Но представления о чувственном опыте, как источнике знаний, сталкиваются с неразрешимым вопросом, когда речь идёт о такой абстрактной науке, как оперирующая символами математика. Особенно значительными были достижения вавилонской математической астрономии. Но внезапный ли скачок поднял месопотамских математиков от уровня утилитарной практики до обширных познаний, позволяющих применять математические методы для предвычисления положений Солнца, Луны и планет, затмений и других небесных явлений, или развитие шло постепенно, мы, к сожалению, не знаем. История математических знаний вообще выглядит странновато.

Нам известно, как наши предки учились считать на пальцах рук и ног, делали примитивные числовые записи в виде зарубок на палке, узелков на верёвке или выложенных в ряд камешков. А далее — без всякого переходного звена — вдруг сведения о математических достижениях вавилонян, египтян, китайцев, индусов и других древних учёных, настолько солидных, что их математические методы выдерживали испытание временем вплоть до середины недавно закончившегося II тысячелетия, т. е. на протяжении более чем трёх тысяч лет…

Что скрыто между этими звеньями? Почему древние мудрецы, помимо практического значения, почитали математику как священное знание, а числам и геометрическим фигурам давали имена богов? Только ли за этим стоит трепетное отношение к Знанию, как таковому? Возможно, придёт время, когда археологи найдут ответы на эти вопросы. А пока ждём, не будем забывать, что ещё 700 лет назад сказал оксвордец Томас Брадвардин: «Тот, кто имеет бесстыдство отрицать математику, должен был бы знать с самого начала, что никогда не войдёт во врата мудрости».